RB-Tree 조건
- 모든 노드는 red/black
- 루트노드는 black
- 모든 NIL 노드는 black
- 노드가 RED면 자식은 BLACK (연속 red x)
- 임의의 노드에서 경로 NIL까지 BLACK 개수 동일

삽입규칙
기본규칙
- 자식 노드의 색이 같을 경우, 부모와 색을 교환할 수 있다.
- 루트노드가 레드라면 블랙으로 바꿀 수 있다.
Case3. RED가 연속되었고, 한쪽으로 몰려있을때

가정.
- 삽입된 노드의 부모가 RED
- 부모의 형제는 BLACK
- 조부모 -> 부모 -> 삽입노드가 같은 방향
반례.
- 이 경우 조부모는 레드일 수 없다.
해결.
- 조부모와 부모의 색을 바꿈
- 반대방향으로 회전
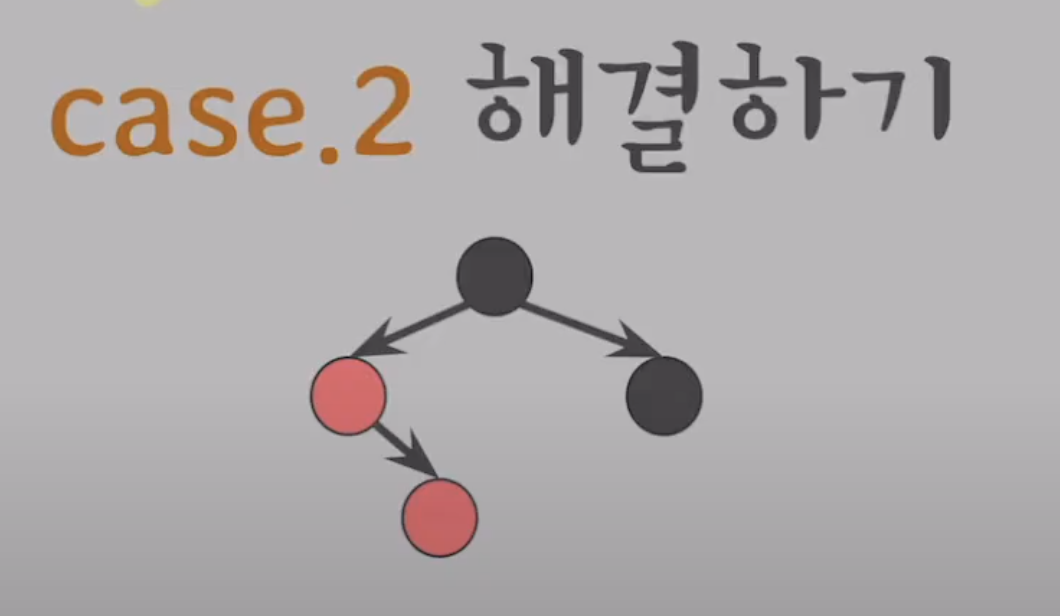
Case2. RED가 연속되었고, 꺾인 방향일 때
가정. - 삽입된 노드의 부모가 RED
- 부모의 형제는 BLACK
- 조부모 -> 부모, 부모 -> 삽입노드가 다른 방향
반례.
- 이 경우 조부모는 레드일 수 없다.
해결.
- 부모와 해당노드를 rotate
- case3번으로 해결
Case1. RED가 연속되었고, 삼촌이 RED일때
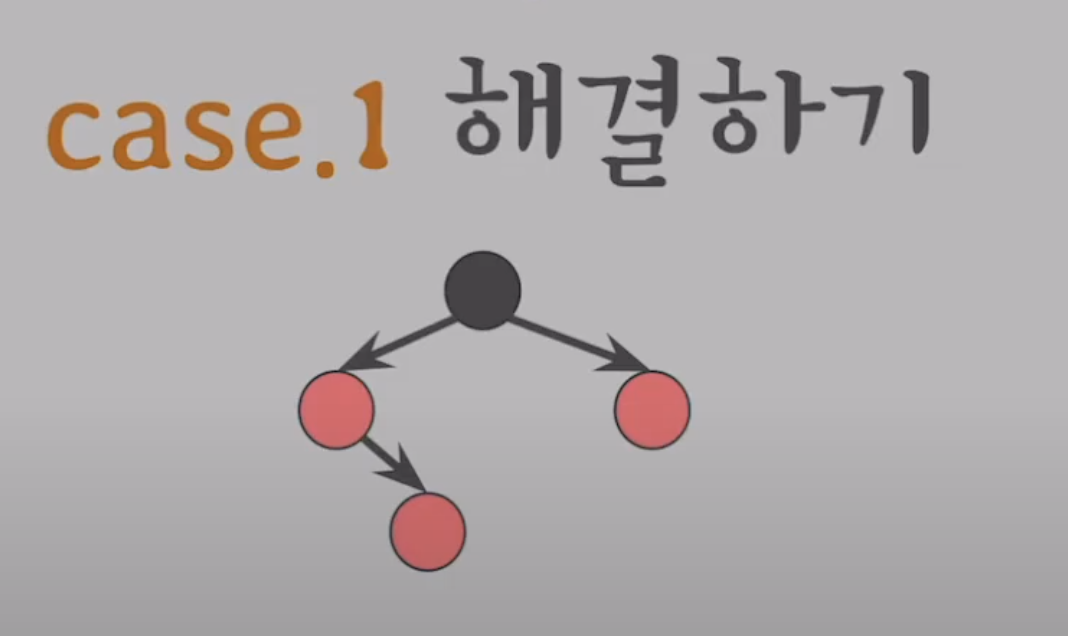
가정.
- 삽입된 노드의 부모가 RED
- 부모의 형제는 RED
- 방향은 어디든 관계없음.
반례.
- 이 경우 조부모는 레드일 수 없다.
해결.
- 두 자녀의 색이 같으면 부모의 색과 바꿔도 무방하다. 를 이용
- 조부모노드 기준으로 규칙확인
삭제규칙
기본규칙
- 삭제하려는 노드의 자녀가 없거나 하나라면
- 삭제되는 색 = 삭제되는 노드의 색
- 삭제하려는 노드의 자녀가 두개라면
- 삭제되는 색 = 삭제되는 노드의 successor의 색
- 여기서 삭제되는 색이 RED라면 그냥 삭제 가능하다.
- 특수상황을 제외하면 모두 extra black을 넣어줘야 한다.
- extra black이란 삭제되는 색을 대체하는 노드에 추가하는 추가black
doubly black = 없애는 방법이 4가지
red-and-black = 그냥 Black으로 바꿔주면 됨
중요한점은 삭제되는 노드의 색과 그 노드를 대체하는 노드에 차이를 둬야 한다.
특수상황
- 루트노드가 RED가 되는 상황이면 그냥 BLACK으로 바꿔주고 끝
doubly black을 없애는 방법 4가지
Case4. 형제가 Black, 같은방향의 형제의 자식이 Red 일경우

목적.
- 형제 자식의 Red를 doubly black의 부모로 옮기자(색만)
해결.
- 오른쪽 형제의 오른쪽자녀 + 왼쪽자녀에게서 레드를 가져온다
- 이때 왼쪽자녀의 색은 모르기 때문에 extrablack을 줌
- 이때 extrablack을 줄 수 있는 이유는 black의 개수를 보존하기 위해서
- 부모와 형제 노드의 색을 바꾸고 회전
- 이제 기존 노드의 형제가 바뀌게 되면서 둘다 extrablack을 가지고 있다.
- 양쪽에서 개수를 -1 씩 하면 끝
결과.
형제는 부모의 색
형제의 같은방향 자녀는 블랙
부모는 블랙으로 바꾼 후에 회전만 하면 끝.
Case3. 형제가 Black, 다른방향 형제의 자식이 Red일 경우
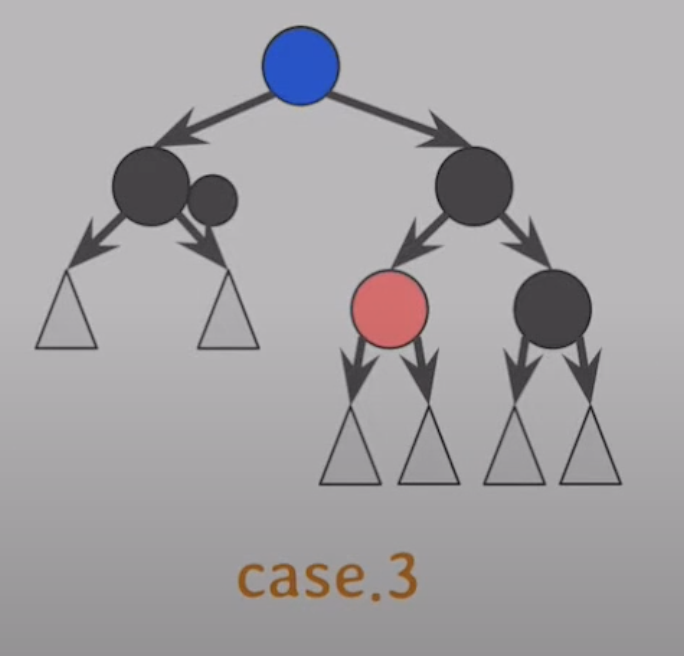
목적.
- 형제 자식의 Red를 doubly black의 부모로 옮기자(색만)
해결.
- 반대방향 형제자식의 Red와 형제의 Black을 바꾼 후 회전
- Case4로 해결
Case2. 형제가 Black, 형제의 자식들도 모두 Black일 경우

목적.
- doubly black과 형제에게서 black을 -1 씩 수행
- 양쪽에서 black이 하나씩 사라졌으니 부모에게 doubly black
- 기존노드는 Black, 형제노드는 Red
- 부모노드를 기준으로 다시 doublyblack삭제 수행
Case1. 형제가 레드일때

해결.
- 형제노드와 부모노드의 색을 바꾼 후 로테이션
- doubly black의 형제노드가 black노드로 새로 생김
- 이 때 case2,3,4 로 해결가능
출처
'Develop' 카테고리의 다른 글
| Pintos_project1 - Alarm Clock (0) | 2025.09.09 |
|---|---|
| malloc lab-implicit list에 관하여 + 구현 (3) | 2025.08.23 |
| [C언어] 포인터, 주소, malloc.. 등등 (5) | 2025.08.08 |
| Longest Common Subsequence (5) | 2025.08.04 |
| 위상정렬 Topological Sort (3) | 2025.07.29 |
