정렬의 종류

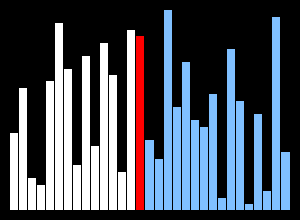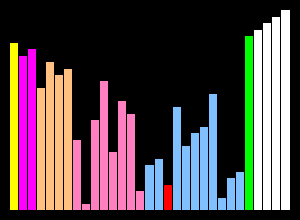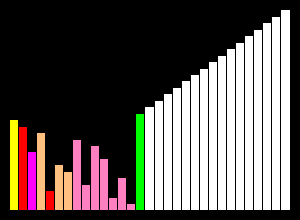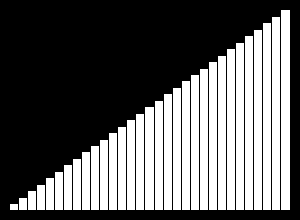
안정성(Stability)이란?

안정 정렬(Stable Sort):

동일한 값을 가진 요소들의 상대적 순서가 정렬 후에도 유지되는 정렬

불안정 정렬(Unstable Sort):

동일한 값을 가진 요소들의 상대적 순서가 바뀔 수 있는 정렬

1. 버블정렬

인접한 두 원소를 비교하여 순서를 바꾸며, 매 순환마다 최대값이 배열의 끝으로 가는 정렬. 거품처럼 올라가는 것처럼 보여서 버블정렬

최적화

1. check 값을 두어 변경이 없었으면 정렬을 멈춤
2. start를 두어 배열의 뒤에서부터 즉, 이미정렬된건 확인하지 않음
   == 속도차이 2배

특징

• 안정성: 안정 정렬 ✅
• 시간복잡도: O(n²)
• 공간복잡도: O(1)

2. 선택 정렬

가장 작은(큰) 원소를 찾아서 맨 앞 위치와 교환하는 방식.
선택한다고 해서 선택정렬

특징

• 안정성: 불안정 정렬 ❌
• 시간복잡도: O(n²)
• 공간복잡도: O(1)

3. 삽입정렬

정렬된 부분에 해당 원소를 삽입

### 특징

• 안정성: 안정 정렬 ✅
• 시간복잡도: O(n²) (최선의 경우 O(n))
• 공간복잡도: O(1)

4. 합병정렬

재귀를 사용하여 원소를 부분집합으로 나눈 후 정렬
부분집합들은 모두 정렬된 상태.

### 특징

• 안정성: 안정 정렬 ✅
• 시간복잡도: O(n log n) (모든 경우)
• 공간복잡도: O(n)
• 알고리즘: 분할 정복 (Divide and Conquer)****

5. 퀵정렬

피벗값을 선택하여 피벗을 기준으로 분할한 후 재귀적으로 정렬

특징

• 안정성: 불안정 정렬 ❌
• 시간복잡도: 평균 O(n log n), 최악 O(n²)
• 공간복잡도: O(log n) (재귀 호출 스택)
• 알고리즘: 분할 정복

6. 힙정렬

특징

• 안정성: 불안정 정렬 ❌
• 시간복잡도: O(n log n) (모든 경우)
• 공간복잡도: O(1)
• 알고리즘: 힙(Heap) 자료구조 활용

비교

알고리즘	안정성	평균 시간복잡도	최악 시간복잡도	공간복잡도	특징
합병 정렬	안정	O(n log n)	O(n log n)	O(n)	예측 가능한 성능
퀵 정렬	불안정	O(n log n)	O(n²)	O(log n)	평균적으로 가장 빠름
힙 정렬	불안정	O(n log n)	O(n log n)	O(1)	메모리 효율적